Kalman Filter (KF)란 무엇인가?

많이 참조한 글,,,

1. 필터링이란 무엇인가?

• 으아아아아아아아아아악

1.1. 칼만 필터는 “현재 상태의 믿을만한 정도(belief)가 가우시안 분포로 나타나는 베이지안 필터”다. 이게 대체 무슨 소리임?

• 우선 ‘베이지안’과 ‘믿을만한 정도’라는 단어부터 짚고 넘어가자.
• 베이즈 정리는 여기에서도 언급했듯 사전 확률과 가능도를 결합하면 사후 확률이 나온다는 정리다.
  • 여기서 사전 확률은 가설 내지는 이미 알고 있던 정보(배경 지식, 상식, 기타등등…)를 나타내는 분포이다. (기상 관측 인공위성이 지금 위치한 곳을 열대지방이라고 가정하자.)
  • 가능도는 특정한 가설에 기반했을 때 어떤 사건이 발생할 가능성을 나타낸다. (위성이 위치한 곳이 열대지방이라면, 여기 눈이 올 확률은 얼마인가?)
  • 사후 확률은 특정한 데이터에 대해서 어떤 가설이 맞을 가능성을 나타낸다. (인공위성의 탐지기에 눈이 오는 것이 관측되었다면, 과연 위성이 있는 곳을 열대지방이라고 말할 수 있는가?)
    • 데이터를 잘 설명하지 못하는 가설일수록 이 확률은 매우 낮을 것이며, 우리가 위성의 위치에 대해 가진 가설을 재고해야 함을 나타낼 것이다.
• 이러한 베이즈 정리가 유추에 적극적으로 활용되는 모델 중 하나로는 은닉 마르코프 모델(hidden Markov model, HMM)이 있다.
  • 참조: HMM
    • 어떤 시스템을 크게 “관측이 불가능한 부분 (state)”과 “관측이 가능한 부분 (observation)”으로 나눈다고 생각하면 편하다.
    • 기본적인 가정은 관측할 수 없는 state에 의해 observable data가 방출(emission)된다는 것이다.
    • 이러한 state가 시간에 따라 변하는(transition) 것까지 고려한다면 마르코프 연쇄(Markov chain, MC)가 된다.
  • 실제 상황에서는 대부분 observable data로부터 state를 유추해야 한다. 따라서 자연히 베이즈 정리가 쓰이게 된다!
  • 이 때 믿을만한 정도(belief)는 관측 가능한 것들로부터 추론한 상태 x가 진짜 상태 x일 가능성을 의미한다. (세상에 믿을 거 하나 없다는 사실을 다시금 되새기게 된다.)
  • 더 구체적으로는, 시간 1부터 t까지 측정한 데이터 z가 있을 때 t에서의 상태 x에 대한 belief를 \(p(x_t \mid z_{1:t})\)로 정의한다.

1.2. 이 베이즈 정리와 필터링은 대체 무슨 상관이 있을까?

• 이 맥락에서 필터(filter)가 정확히 뭘 뜻하는 것일까?
  • 신호나 시스템 관련 수업에서 주파수 대역 필터링 같은 건 많이 들어봤는데… 이것보다 좀 더 넓은 개념인 것 같다. 물론 HEPA 필터와 같은 물리적 필터도 아니다.
  • 사진이나 음성을 보정할 때 쓰는 노이즈 필터는 관련이 있을 수도 있겠다. 여기에서 필터링은 내가 “관측값을 믿지 못하겠을 때” 거치는 과정 전반을 의미한다.
    • 이를테면 다음 그림과 같이 네비게이션이 GPS 신호를 통해 차량의 실시간 위치를 관측해서 화면 상에 표시하고 있다고 생각해보자.
    
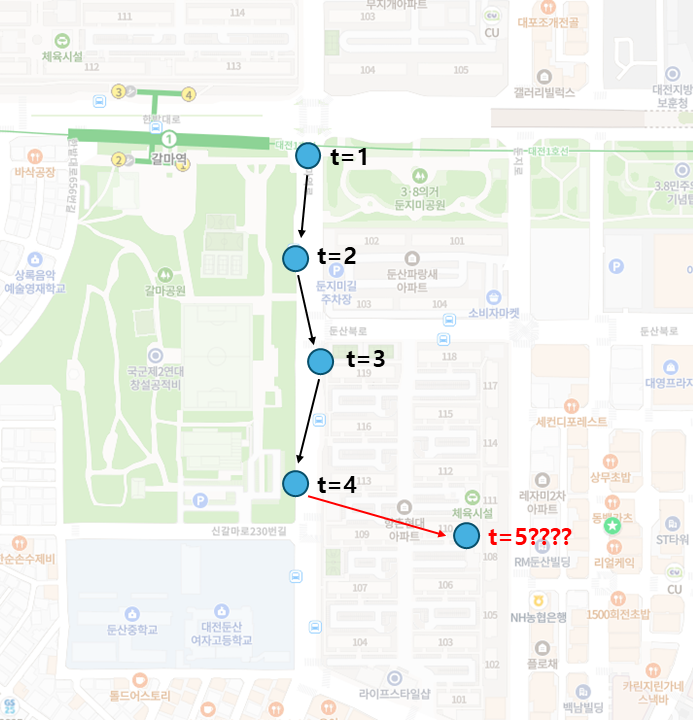
    • 연속된 시간 t=1에서 4까지는 GPS로 관측된 신호가 그럭저럭 멀쩡한 것으로 보인다. 그러나 t=5에서는 차가 갑자기 아파트 한가운데에 있는 것으로 나타난다.
    • 차가 하늘을 날아서 실제로 저 위치까지 갔을까? 아니면 단순히 GPS 신호의 일시적 오류(또는 잡음, noise)일 뿐일까? 당연히 후자다.
    • 그런데 당연히 후자가 맞을 것이라는 확신은 어디에서 나올까? 바로 이전까지 관측된 정보(z)에서 나온다. (물론 우리의 상식(h)도 작용했을 것이다)
  • 이처럼 현 시점의 관측값을 곧이곧대로 “믿지 못하는” 경우는 생각보다 자주 발생하기 때문에, 이미 관측된 데이터임에도 다시금 추정을 해야 하는 상황이 발생할 수 있다.
    • 그리고 위에서도 언급했듯 어떤 데이터에 노이즈가 끼어있다는 확신(거꾸로 말하자면 새로 얻은 데이터에 대한 낮은 belief)은 이전까지의 정보를 통해서 얻어지기 때문에 베이즈 추론과 관련이 있는 것이다.
    • (다만 모든 필터가 베이즈 추론을 사용하는 것은 아니다. 예를 들면 이미지나 음성에 적당한 커널을 일괄적으로 곱해서 처리하는 것은 필터링은 맞지만 베이지안은 아닐 수 있다.)
• 참고로, filtering 이외에도 관측 데이터에 대해서 다양한 추정 문제가 존재한다. (Smoothing, prediction, interpolation 등)
  • 어차피 다 나중에 알아야 할 것들이라서 메모해둠,,,

1.3. 그럼 베이지안 필터란 정확히 무엇인가?

• 위 내용을 정리하면, 베이즈 필터는 이산 확률 과정의 연쇄(예를 들면, 단위 시간마다 측정한 차량의 위치의 확률분포)에서, 이전 상태로부터 현재 상태를 추정함으로써 현재 상태를 검증하는 과정이라고 볼 수 있겠다.
  • 이 때 t에서 추정한 posterior는 다음 step, 즉 t+1로 업데이트가 되면 prior를 계산할 때 쓰인다. (더 정확히 말하자면 belief가 이러하다.)
  • 따라서 베이즈 필터는 재귀적(recursive)이라고 불리기도 한다.
• 구체적으로 살펴보면, 시간에 따라 연쇄적으로 변하는 state와 observable data에 대해서 다음과 같은 시스템 모델을 정의할 수 있다.
  • 어떤 시점 t에서 state x에 영향을 주는 input: \(u_t\)
  • 시점 t에서 시스템의 state, 보통 관측할 수 없음: \(x_t\)
  • 시점 t에서 state x에 있는 시스템이 출력하는 output, 관측 가능함: \(z_t\)
• 그리고 \(u_{t-1}\) → \(z_{t-1}\) → \(u_{t}\) → \(z_{t}\) → … 의 input과 observation이 반복될 때, 시스템의 state에 대한 분포 및 그에 대한 belief는 다음과 같이 변한다.
  • 이전 state 및 현재의 input이 주어졌을 때 현재 state로 추정되는 것: \(p(x_t \mid u_t, x_{t-1})\)
  • 이전 state까지만 보고 추정한 지금 상태 \(x_t\)에 대한 belief: \(\overline{bel}(x_t)\)
  • 현재 state에서 observe할 수 있는 output: \(p(z_t \mid x_t)\)
  • 현재의 output z까지 보고 추정한 지금 상태 \(x_t\)에 대한 belief: \(bel(x_t)\)
    • 정의에 따르면, \(bel(x_t) = p(x_t \mid z_{1:t}, u_{1:t})\) 이다. 하지만 이것을 단숨에 계산하기는 어렵다.
    • 그러니 우선 귀납적으로 계산해보기 위해 베이즈 정리를 적용하여 \(=\eta \cdot p(z_t \mid x_t, z_{1:t-1}, u_t) \cdot p(x_t \mid z_{1:t-1}, u_{1:t})\) 로 분리해보자. 이는 위의 식에서 z를 \(z_t\)와 \(z_{1:t-1}\)로 분리한 것과 같다.
    • 여기서 다음과 같은 Markov assumption을 적용하고자 한다.
      • 시간에 따른 모든 u가 서로 독립이고, 마찬가지로 z가 독립이라고 가정.
      • 그리고 모든 사전 정보는 \(bel(x_{t-1})\)에 함축되어 있으며, 현재 state \(x_t\)는 오직 \(x_{t-1}\)의 영향만 받는다고 가정.
      • 그러면 \(z_t\)는 애초에 \(z_{1:t-1}, u_t\)와는 무관하므로, \(p(z_t \mid x_t)\)가 된다.
      • 즉 \(= \eta \cdot p(z_t \mid x_t) \cdot p(x_t \mid z_{1:t-1}, u_{1:t})\)
    • 그리고 state x에 대해 law of total probability를 적용해, \(p(x_t \mid z_{1:t-1}, u_{1:t})\)를 이전 state에 대한 적분으로 나타낼 수 있다.
      • \[p(x_t \mid z_{1:t-1}, u_{1:t}) = \int_{x_{t-1}} p(x_t \mid x_{t-1}, z_{1:t-1}, u_{1:t}) \cdot p(x_{t-1} \mid z_{1:t-1}, u_{1:t}) dx_{t-1}\]
      • 그리고 다시 Markov assumtion을 적용하면, 첫 번째 항에서 z와 u를 없앨 수 있다. (\(p(x_t \mid x_{t-1}, z_{1:t-1}, u_{1:t}) = p(x_t \mid x_{t-1})\))
      • 또한 이전 state는 현재 input의 영향을 받지 않으니 두 번째 항에서 \(u_t\)를 없애고 \(u_{1:t-1}\)로 쓸 수 있다.
      • 즉 \(= \eta \cdot p(z_t \mid x_t) \int_{x_{t-1}} p(x_t \mid x_{t-1}) \cdot p(x_{t-1} \mid z_{1:t-1}, u_{1:t-1}) dx_{t-1}\)
    • 이렇게 되면, 적분의 두 번째 항이 \(bel(x_{t-1})\)의 정의와 일치하게 된다.
      • 즉 \(= \eta \cdot p(z_t \mid x_t) \int_{x_{t-1}} p(x_t \mid x_{t-1}) \cdot bel(x_{t-1}) dx_{t-1}\)
    • 또한 적분 식 전체는 해석해보면 이전 state까지만 보고 추정한 지금 상태에 대한 belief, 즉 \(\overline{bel}(x_t)\)에 해당한다.
    • 따라서 최종적으로는 \(bel(x_t) = \eta \cdot p(z_t \mid x_t) \cdot \overline{bel}(x_t)\)와 같은 식이 성립한다!
      • 이를 말로 해석하자면 “이전까지의 정보만 가지고 현재 상태를 해석한 \(\overline{bel}(x_t)\)가 있을 때, 현재 관측한 \(p(z_t \mid x_t)\)를 사용하여 correction한 결과가 현재 state에 대한 belief \(bel(x_t)\)가 된다”는 뜻이다.

2. Kalman Filter

• Kalman filter는 위 과정에서 쓰이는 확률 분포가 Gaussian인 경우를 의미한다.
  • 이전 글에서도 언급했듯 prior와 posterior의 (그리고 경우에 따라 likelihood까지) 분포가 모두 같으면 계산이 (특히 적분이!!) 매우 쉽다. Gaussian (normal) distribution은 그 조건을 만족한다.
• 위에서 설명한 베이지안 필터의 개념을 더 정확한 수식으로 만들기 위해 다음과 같은 state transition 모델을 가정하자. (참조)
  • (1) 사용자가 input을 입력하는 control-input model \(B_t\)와 input \(u_t\)
  • (2) 사용자가 (정확히는 알 수 없지만) hidden state의 변화를 가정하는 state-transition model \(F_t\)와 process noise의 covariance \(Q_t\)
  • (3) 사용자가 output을 관측하는 observation model \(H_t\)와 observation \(z_t\), 그리고 observation noise의 covariance \(R_t\)
  • (4) 관측할 수 없는 hidden state \(x_t\), process noise \(w_t\), observation noise \(v_t\), 그리고 예측의 정확도를 나타내는 estimate covariance \(P_t\)
• 그러면 state x 및 observation z에 대한 계산식은 각각 다음과 같다.
  • \[x_t = F_t x_{t-1} + B_t u_t + w_t\]
  • \[z_t = H_t x_t + v_t\]
• Kalman filter는 다음과 같은 두 단계를 반복해 재귀적으로 현재의 값을 추정한다.
  • (1) 예측 단계 (Prediction)
    • State에 대한 예측, 즉 \(\overline{bel}(x_t)\)를 계산하는 단계이다.
      • 여기까지는 오직 t-1까지 얻은 정보로만 추론을 하기 때문에, 이 시점에서 state에 대한 믿음을 \(\hat{x}_{t \mid t-1}\)로 쓰기도 한다.
    • Predicted state estimate: \(\overline{bel}(x_t) = F_t bel(x_{t-1}) + B_t u_t + w_t\)
      • Predicted estimate covariance: \(P_{t \mid t-1} = F_t P_{t-1 \mid t-1} F_{t}^{T}+Q_{t-1}\)
    • Observation: \(z_t = H_t x_t + v_t\)
      • x_t는 아직 모른다. 우리가 알거나 가정한 것은 z_t와 H_t 뿐이다.
  • (2) 보정 단계 (Update)
    • 예측(\(\overline{bel}(x_t)\)) 분포와 관측(\(p(z_t \mid x_t)\)) 분포를 합해서 현재 state에 대한 믿음을 보정(\(bel(x_t)\))하는 단계이다.
      • 개념적으로는 이해하겠는데, 어떻게 합친다는 걸까? 관측할 수 있는 observation과, 앞서 예측한 x에서 나올 수 있는 결과인 (optimal) forecast를 비교하는 방식이다.
    • 우선 observation과 forecast의 차이는 잔차(residual)이라고 부르며, \(y_{t \mid t-1}\)로 쓴다.
      • 이는 \(y_{t \mid t-1} = z_t - H_t \overline{bel}(x_t)\)로 구할 수 있다.
      • 그리고 여기에 대한 covariance는 \(S_t = H_t P_{t \mid t-1} H_{t}^{T}+R_t\)이다. 위의 estimate covariance와 식이 매우 비슷하다.
      • 이를 mesurement pre-fit residual이라고도 한다. 말 그대로 fit 이전에 ‘예측만으로 구해본 forecast가 observation과 얼마나 차이나는지’에 대한 추정치라는 뜻이다.
    • \(P_{t \mid t-1}\) (prediction의 covariance), \(H_t\) (observation model), \(S_t\) (observation과 forecast의 차이의 covariance)를 모두 알고 있으므로 Kalman gain을 계산할 수 있다.
      • Kalman gain(\(K_t\))은 ‘내 예측과 관측 결과 중 무엇을 더 믿을지’의 가중치를 결정한다.
        • Gain이 0이면, 나는 내가 observation을 보기 전에 예측한 state만을 믿는다.
        • Gain이 1이면, observation만을 믿는다.
        • 즉 \(K_t\)를 실제 update에 적용했을 때의 식을 살짝 미리보기 하면 \(bel(x_t) = \overline{bel}(x_t) + K_t \cdot (y_{t \mid t-1})\) 가 된다.
      • 정의 및 차원이 맞으려면 \(K_t\)의 식은 어때야 할까?
        • 우선 y의 차원은 결국 observation과 같기 때문에, K의 계산은 기본적으로 observation model인 H에서 시작한다.
        • Kalman gain은 작아질수록 observation을 신뢰하지 않는다. 따라서 y에 대한 covariance인 S로 나눠준다. (즉 역행렬을 곱한다.)
          • S = HPH + R이므로, 즉 observation의 covariance R이 커질수록 K는 줄어들게 된다. observation이 불확실하다는 뜻이다.
        • 그리고 Kalman gain은 커질수록 나의 기존 estimation을 신뢰하지 않는다. 따라서 \(\overline{bel}(x_t)\)에 대한 prediction covariance P를 곱한다.
          • 즉 prediction의 covariance P가 클수록 K가 1에 가까워져야 한다. 나의 기존 (observation을 까보기 이전의) estimation이 불확실하다는 뜻이다.
      • 결론적으로 Kalman gain의 식은 \(K_t = P_{t \mid t-1} H_{t}^{T} S_{t}^{-1}\) 이다.
    • 그리고 관측을 반영하여 새로 계산한 state (updated predicted state estimate) \(x_t\)는 앞서 언급했듯 \(bel(x_t) = \overline{bel}(x_t) + K_t \cdot (y_{t \mid t-1})\)가 된다.
      • t에서 새로 얻은 정보를 사용했으므로, 새로이 계산한 state에 대한 믿음을 \(\hat{x}_{t \mid t}\)로 쓰기도 한다.
    • 마지막으로, 관측을 반영하여 새로 계산한 state에 대한 covariance (updated predicted estimate variance) \(P_{t \mid t} = (I - K_t H_t)P_{t \mid t-1}\)이다.
• 결국 핵심은 (1) \(\overline{bel}(x_t)\)를 계산하고, (2) \(K_t\)를 계산하고, 이를 바탕으로 (3) \(bel(x_t)\)를 계산하는 것이다.
  • 앞서 언급했듯 칼만 필터는 가우시안 분포에 대한 베이지안 필터이므로, 1D 또는 multivariate Gaussian distribution을 대입해주면 구체적인 값을 계산할 수 있다.
  • 만약 1D Gaussian 분포에 대한 1D Kalman filter를 계산하고자 한다면, estimate는 분포의 mean(\(\mu\))이고, uncertainty 또는 covariance는 분포의 variance(\(\sigma^2\))라고 생각하며 계산하면 된다.
• 예를 들어, 1D Kalman filter에 대한 prediction 및 update는 다음과 같다.
  • (1) Prediction
    • Predicted state estimate: \(\overline{bel}(x_t) = \overline{\mu}_{x, t} = \mu_{x, t-1} + u_t\)
    • Predicted estimate variance: \(\overline{\sigma}_{P, t}^2 = \sigma_{P, t-1}^2 + \sigma_{Q, t}^2\)
      • 여기서 P는 state에 대한 variance, Q는 process(motion, transition 등등…)에 대한 variance임을 의미한다. 위 식과 비교하기 쉬우라고 저렇게 씀…
  • (2) Update
    • Kalman gain: \(K_t = \frac{\overline{\sigma}_{P, t}^2}{\overline{\sigma}_{P, t}^2+\overline{\sigma}_{R, t}^2}\)
      • R은 마찬가지로 해당 σ가 observation에 대한 variance임을 의미한다. 아 그냥 xyz로 통일할걸… 너무 먼 길을 옴
    • Updated predicted state estimate: \(bel(x_t) = \mu_{x, t} = \overline{\mu}_{x, t} + K_t (\mu_{z, t} - \overline{\mu}_{x, t})\)
    • Updated predicted estimate variance: \(\sigma_{P, t}^2 = (1-K_t) \overline{\sigma}_{P, t}^2\)

3. Particle Filter

• Particle filter는 확률 분포가 가우시안 분포가 아닌 일반적인 경우에 대해, 랜덤 샘플링을 통해서 확률 분포를 모사하여 필터링을 적용하는 과정을 의미한다.
  • 물론 가우시안 분포인 경우에도 적용이 가능하다. 핵심적인 것은 선형 모델 뿐만 아니라 비선형 모델에도, 가우시안 분포가 아닌 다른 일반적인 분포에도 “일반화”가 가능하다는 점이다.
• 더 구체적으로는, \(bel(x_t)\)를 직접 계산할 수 없기 때문에 \(x_t\)를 샘플링한 집합 \(\hat{x}_t\)로 표현하는 방법이다.
  • 확률 분포를 이용한 베이지안 필터에서 모델의 state에 대한 믿음 \(bel(x_t)\)는 확률 분포로 나타난다.
    • “확률 분포로 나타난다”는 것은 이 state variable을 확률 분포에 대한 hyperparameter (예를 들어 가우시안 분포의 경우 평균과 표준편차)로 나타낼 수 있다는 뜻이다.
    • 가령 어떤 모델의 state variable이 “위치”일 경우, 1D Gaussian \(bel(x_t)\)는 예상되는 위치를 mean으로 하고 그 주변 반경 \(\sigma\)만큼을 표준편차로 하는 원형 공간으로 나타날 것이다.
  • 반면 particle filter에서는

4. 논문 읽음

• 읽으려 한 논문 1: Kim, Lee, Forger (2023)
• 읽으려 한 논문 2: Bonarius, Papatsimpa, Linnartz (2021)